De EncyclopAtys
m (→La réalité (en jeu)) |
m |
||
| (7 révisions intermédiaires par 2 utilisateurs non affichées) | |||
| Ligne 1 : | Ligne 1 : | ||
| − | {{ | + | <noinclude>{{Trad |
| − | + | |DE=Arcueid's Handwerks-Anleitungen/Handwerk und Materialien |DEs=4 | |
| − | + | |EN=Arcueid's Crafting Guides/Crafting and Materials |ENs=0 | |
| + | |ES=Las Guías de Artesanía de Arcueid/Artesanía y materiales |ESs=0 | ||
| + | |FR=Guides d'artisanat d'Arcueid/Artisanat et matériaux |FRs=1 | ||
| + | |RU=Крафтовые гиды по Arcueid/Крафт и материалы |RUs=1 | ||
| + | |palette=OOC | ||
| + | }}</noinclude> | ||
== Définitions == | == Définitions == | ||
'''Moyenne''' | '''Moyenne''' | ||
| Ligne 10 : | Ligne 15 : | ||
=== Grades === | === Grades === | ||
| − | Il existe 5 grades de matériaux dans Ryzom et | + | Il existe 5 grades de matériaux dans Ryzom et chacune a une valeur moyenne qui lui est attribuée. Si vous regardez un matériau d'une qualité donnée et que vous calculez la valeur moyenne de ses statistiques, vous obtiendrez la liste suivante : |
* 20 pour la catégorie de base | * 20 pour la catégorie de base | ||
| − | * 35 pour | + | * 35 pour Fin |
| − | * 50 pour le | + | * 50 pour le Choix |
* 65 pour Excellent | * 65 pour Excellent | ||
* 80 pour les Suprêmes | * 80 pour les Suprêmes | ||
| − | Ces valeurs déterminent également le | + | Ces valeurs déterminent également le qualité d'un objet artisanal. Si vous calculez la valeur moyenne des statistiques qu'un objet artisanal affiche dans l'aperçu et que vous la comparez au tableau ci-dessus, vous pouvez déterminer la qualité de l'objet. Si votre valeur moyenne est supérieure à la moyenne du grade, la qualité sera celui du grade supérieur suivant. Par exemple, si votre moyenne se situe entre 51 et 65, la qualité sera Excellent. S'il est à 50, il sera Choix. Cela semble fonctionner dans la plupart des cas, mais il y a eu quelques exceptions à la règle en raison des arrondis ou d'autres problèmes. |
=== Statistiques sur les matériaux === | === Statistiques sur les matériaux === | ||
| − | Toutes les matières premières suivent certaines règles sur la façon dont leurs statistiques sont structurées. Il y a toujours une valeur supérieure à toutes les autres et deux valeurs inférieures à toutes les autres. Les | + | Toutes les matières premières suivent certaines règles sur la façon dont leurs statistiques sont structurées. Il y a toujours une valeur supérieure à toutes les autres et deux valeurs inférieures à toutes les autres. Les valeurs restantes se situent entre ces extrêmes et sont égales en nombre. La valeur la plus élevée est supérieure de 40 à la moyenne et les deux valeurs les plus basses sont inférieures de 20 à la moyenne. Elles s'annulent mutuellement, puisque +40 -20 -20 est égal à 0. L'article a une valeur moyenne parfaite et correspond au graphique. Jusqu'à présent, tout va bien. (Ou excellent ?) |
| Ligne 29 : | Ligne 34 : | ||
{{Clear}} | {{Clear}} | ||
| − | === Exemple : Graine suprême ( | + | === Exemple : Graine suprême (parure de bijoux) === |
Il comporte 7 statistiques : 1x haut à 100, 2x bas à 60 et le reste de ses valeurs à la moyenne de la note suprême, qui est de 80. Calculons la moyenne de la matière en tenant compte des valeurs limites (1x 100 + 2x 60 + 4x 80) divisée par 7, soit 77,1 ! Mais elle aurait dû être de 80 selon la théorie. Le matériau est 3% plus mauvais qu'il ne devrait l'être ! Pour corriger cela, les valeurs des statistiques du milieu ont été modifiées dans le jeu de 80 à 85 (1x 100 + 2x 60 + 4x 85) divisé par 7 est 80. Et voilà ! | Il comporte 7 statistiques : 1x haut à 100, 2x bas à 60 et le reste de ses valeurs à la moyenne de la note suprême, qui est de 80. Calculons la moyenne de la matière en tenant compte des valeurs limites (1x 100 + 2x 60 + 4x 80) divisée par 7, soit 77,1 ! Mais elle aurait dû être de 80 selon la théorie. Le matériau est 3% plus mauvais qu'il ne devrait l'être ! Pour corriger cela, les valeurs des statistiques du milieu ont été modifiées dans le jeu de 80 à 85 (1x 100 + 2x 60 + 4x 85) divisé par 7 est 80. Et voilà ! | ||
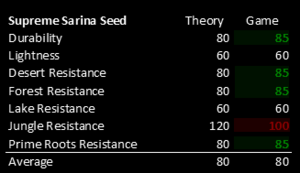
[[File:Comparison of theory and ingame stats.png|thumb|left|Comparison de la théorie et des stats en jeu pour des graines Supreme Sarina]] | [[File:Comparison of theory and ingame stats.png|thumb|left|Comparison de la théorie et des stats en jeu pour des graines Supreme Sarina]] | ||
| − | + | {{Clear}} | |
| − | Règle générale : le montant de la correction nécessaire pour les statistiques intermédiaires dépend du nombre total de statistiques dont dispose un matériel. Examinons les deux extrêmes dans les paragraphes suivants, | + | Règle générale : le montant de la correction nécessaire pour les statistiques intermédiaires dépend du nombre total de statistiques dont dispose un matériel. Examinons les deux extrêmes dans les paragraphes suivants, munitions avec 4 stats et Concentration magie avec 11 stats. |
| − | === Exemple : | + | === Exemple : Munitions (Dent suprême de Capryni) === |
Il ne possède que 4 attributs. Si nous calculons la moyenne, nous obtenons :(1x 100 + 2x 60 + 1x 80) divisé par 4 est 75. Pour corriger cela, nous devons ajouter 20 à la statistique du milieu, en la faisant passer de 80 à 100 ! On obtient alors :(1x 100 + 2x 60 + 1x 100) divisé par 4, soit 80. Parfait ! Le matériel semble avoir deux statistiques élevées maintenant, mais en réalité il n'y a qu'une statistique élevée et une statistique moyenne, qui a été ajustée pour compenser la mauvaise moyenne. | Il ne possède que 4 attributs. Si nous calculons la moyenne, nous obtenons :(1x 100 + 2x 60 + 1x 80) divisé par 4 est 75. Pour corriger cela, nous devons ajouter 20 à la statistique du milieu, en la faisant passer de 80 à 100 ! On obtient alors :(1x 100 + 2x 60 + 1x 100) divisé par 4, soit 80. Parfait ! Le matériel semble avoir deux statistiques élevées maintenant, mais en réalité il n'y a qu'une statistique élevée et une statistique moyenne, qui a été ajustée pour compenser la mauvaise moyenne. | ||
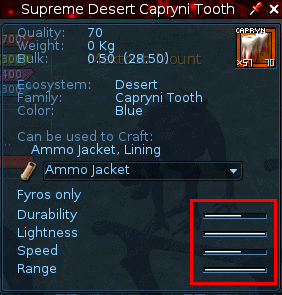
[[File:Supreme Desert Capryni Tooth information.png|thumb|left|Capture d'écran de la fenêtre d'information d'une dent suprême de Capryni du désert ]] | [[File:Supreme Desert Capryni Tooth information.png|thumb|left|Capture d'écran de la fenêtre d'information d'une dent suprême de Capryni du désert ]] | ||
| − | + | {{Clear}} | |
| − | === Exemple : Magic | + | === Exemple : Amplificateur Magic (Ambre Beng Suprême) === |
| − | Il possède 11 attributs. Si nous calculons la moyenne, nous obtenons : (1x 100 + 2x 60 + 8x 80) divisé par 11 donne 78,2. | + | Il possède 11 attributs. Si nous calculons la moyenne, nous obtenons : (1x 100 + 2x 60 + 8x 80) divisé par 11, cela donne 78,2. C'est proche ! C'est la valeur la plus proche que nous puissions obtenir de la moyenne idéale. Elle nécessite le plus petit montant de correction, de 80 à 82. (1x 100 + 2x 60 + 8x 82) divisé par 11 donne 79,6. Le même principe s'applique aux matériaux excellents, la fourchette pour l'état moyen étant dans ce cas de 65 à 70. Pourquoi est-ce important ? Parce qu'une fois que les matériaux Excellent et Suprême sont utilisés, les moyennes idéales pour les notes ne correspondent plus au jeu. Les moyennes sont un facteur important pour les valeurs dans la fenêtre de prévisualisation de l'artisanat, il est donc bon de garder cela à l'esprit. |
<br /> | <br /> | ||
<br /> | <br /> | ||
Merci pour votre lecture ! | Merci pour votre lecture ! | ||
| + | |||
| + | <br /> | ||
| + | <noinclude><br /> | ||
| + | ---- | ||
| + | <small><references/></small> | ||
| + | ---- | ||
| + | {{Simple Banner<!-- | ||
| + | -->| text= <small>[[Guides d'artisanat d'Arcueid]]<br />[[Guides d'artisanat d'Arcueid/Artisanat et couleurs|Artisanat et couleurs]] <small><small>⚪</small></small> [[Guides d'artisanat d'Arcueid/Artisanat et matériaux|Artisanat et matériaux]] <small><small>⚪</small></small> [[Guides d'artisanat d'Arcueid/Artisanat et mathématiques|Artisanat et mathématiques]]</small> <!-- | ||
| + | -->| palette= OOC}} | ||
| + | {{portail|Gameplay|Craft}} | ||
| + | |||
| + | {{last version link|Guides d'artisanat d'Arcueid/Artisanat et matériaux}}</noinclude> | ||
Version actuelle datée du 19 septembre 2021 à 22:33
Sommaire
Définitions
Moyenne
Additionnez les nombres donnés et divisez la somme par leur nombre. Exemple : 8 + 5 + 17 = 30, puis divisez 30 par 3 pour obtenir une moyenne de 10.
Théorie
Grades
Il existe 5 grades de matériaux dans Ryzom et chacune a une valeur moyenne qui lui est attribuée. Si vous regardez un matériau d'une qualité donnée et que vous calculez la valeur moyenne de ses statistiques, vous obtiendrez la liste suivante :
- 20 pour la catégorie de base
- 35 pour Fin
- 50 pour le Choix
- 65 pour Excellent
- 80 pour les Suprêmes
Ces valeurs déterminent également le qualité d'un objet artisanal. Si vous calculez la valeur moyenne des statistiques qu'un objet artisanal affiche dans l'aperçu et que vous la comparez au tableau ci-dessus, vous pouvez déterminer la qualité de l'objet. Si votre valeur moyenne est supérieure à la moyenne du grade, la qualité sera celui du grade supérieur suivant. Par exemple, si votre moyenne se situe entre 51 et 65, la qualité sera Excellent. S'il est à 50, il sera Choix. Cela semble fonctionner dans la plupart des cas, mais il y a eu quelques exceptions à la règle en raison des arrondis ou d'autres problèmes.
Statistiques sur les matériaux
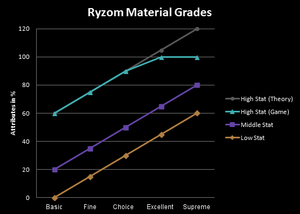
Toutes les matières premières suivent certaines règles sur la façon dont leurs statistiques sont structurées. Il y a toujours une valeur supérieure à toutes les autres et deux valeurs inférieures à toutes les autres. Les valeurs restantes se situent entre ces extrêmes et sont égales en nombre. La valeur la plus élevée est supérieure de 40 à la moyenne et les deux valeurs les plus basses sont inférieures de 20 à la moyenne. Elles s'annulent mutuellement, puisque +40 -20 -20 est égal à 0. L'article a une valeur moyenne parfaite et correspond au graphique. Jusqu'à présent, tout va bien. (Ou excellent ?)
La réalité (en jeu)
Si nous prenons la théorie ci-dessus et l'appliquons à un matériau Excellent, nous obtenons une valeur statistique élevée de 65 + 40 = 105. Pour un matériau Suprême, c'est même 80 + 40 = 120 ! Cependant, tous les matériaux sont limités à des valeurs comprises entre 0 et 100, donc ceux-ci sont simplement coupés dans le jeu... Cela pose-t-il un problème ? Oui, malheureusement, c'est un problème. Si nous calculons les moyennes avec ces nouvelles valeurs, les hauts et les bas ne s'annulent plus. La moyenne du matériau est plus basse qu'elle ne devait l'être, le matériau est déformé.
Exemple : Graine suprême (parure de bijoux)
Il comporte 7 statistiques : 1x haut à 100, 2x bas à 60 et le reste de ses valeurs à la moyenne de la note suprême, qui est de 80. Calculons la moyenne de la matière en tenant compte des valeurs limites (1x 100 + 2x 60 + 4x 80) divisée par 7, soit 77,1 ! Mais elle aurait dû être de 80 selon la théorie. Le matériau est 3% plus mauvais qu'il ne devrait l'être ! Pour corriger cela, les valeurs des statistiques du milieu ont été modifiées dans le jeu de 80 à 85 (1x 100 + 2x 60 + 4x 85) divisé par 7 est 80. Et voilà !
Règle générale : le montant de la correction nécessaire pour les statistiques intermédiaires dépend du nombre total de statistiques dont dispose un matériel. Examinons les deux extrêmes dans les paragraphes suivants, munitions avec 4 stats et Concentration magie avec 11 stats.
Exemple : Munitions (Dent suprême de Capryni)
Il ne possède que 4 attributs. Si nous calculons la moyenne, nous obtenons :(1x 100 + 2x 60 + 1x 80) divisé par 4 est 75. Pour corriger cela, nous devons ajouter 20 à la statistique du milieu, en la faisant passer de 80 à 100 ! On obtient alors :(1x 100 + 2x 60 + 1x 100) divisé par 4, soit 80. Parfait ! Le matériel semble avoir deux statistiques élevées maintenant, mais en réalité il n'y a qu'une statistique élevée et une statistique moyenne, qui a été ajustée pour compenser la mauvaise moyenne.
Exemple : Amplificateur Magic (Ambre Beng Suprême)
Il possède 11 attributs. Si nous calculons la moyenne, nous obtenons : (1x 100 + 2x 60 + 8x 80) divisé par 11, cela donne 78,2. C'est proche ! C'est la valeur la plus proche que nous puissions obtenir de la moyenne idéale. Elle nécessite le plus petit montant de correction, de 80 à 82. (1x 100 + 2x 60 + 8x 82) divisé par 11 donne 79,6. Le même principe s'applique aux matériaux excellents, la fourchette pour l'état moyen étant dans ce cas de 65 à 70. Pourquoi est-ce important ? Parce qu'une fois que les matériaux Excellent et Suprême sont utilisés, les moyennes idéales pour les notes ne correspondent plus au jeu. Les moyennes sont un facteur important pour les valeurs dans la fenêtre de prévisualisation de l'artisanat, il est donc bon de garder cela à l'esprit.
Merci pour votre lecture !
| Guides d'artisanat d'Arcueid Artisanat et couleurs ⚪ Artisanat et matériaux ⚪ Artisanat et mathématiques |